ネイピアの計算棒　ネイピアの骨

ネイピアの計算棒とは
　対数でおなじみの、スコットランドの数学者、ジョン　ネイピア　が
1614年に考案した計算用具で掛け算　割り算　の他、
平方根　立方根も、求められる、なかなかの優れ物です、
さながら西洋判の算木と言ったところでしようか。

ヨーロッパではこの計算具は重宝されたようで、様々な派生形が作られ、
ウイリアム　シッカートがネピアの計算棒にダイアル、
歯車等を付けた計算機を開発し、その頂点に達します、

　しかし、1800年代になると、アリスモメートル計算機、オドナー計算機等
の機械式計算機が、発達し、ネピアの計算棒の時代は終わりを告げます。

ネイピアの計算棒のしくみ
　0～9までの棒があり、それぞれの棒には、掛け算の九九が、上から順
書き込まれています、九九の答には、二桁のものも、ありますが、
一の位と十の位は斜線で分けられています、
これが大変重要なところで、このおかげで、上手く、桁が上がるのです。

掛け算

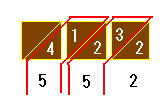
4X138=552　を計算してみます、
計算棒　1と3と8を並べます、
上から4段目の　X４水平列に注目、
それぞれ斜線に囲まれた隣り同士の
マスの数を足していくと、答え 552
が得られます。

次に、24X138=3312では、どうなるのでしょう
24X138=(4X138)+(20X138)　と
書き換えられるので

4X138=552　　　次に
2X138=276　　　を計算します、この末尾に0を付けて
20X138=2760

　　　　　　　４Ｘ１３８＝　５５２
　　　　　　２０Ｘ１３８＝２７６０
　　　　　　　　　　計　　３３１２　　

が求められます。

この様にして、何桁同士の掛け算でも
単純な足し算に変換して計算出来るのです。

しかし、よく考えてみると、これは小学生が習う
九九を使った筆算と同じだと言えます
小学生は九九という一桁の積の一覧表を頭の中に持っていて
この中から必要な物を取りだして計算するのに対して
ネピアは棒に一覧表を備えている、と言えます。

割り算

　ネピアの計算棒では、割り算の答えを直接出すことはできません、
二一天作と言う訳にはいかなくて、小学生の筆算と同じく
掛け算の応用で計算します
1230÷5のような一桁で割るときは計算棒の出番は無いのですが
7224÷28のように、二桁以上の数で割る時、威力を発揮します、

計算棒2と8を並べます

　　　　　　　　　　２　　　　　　　　　　　　　　　　・
　　２　８　) 　７　２　２　４
　　　　　　　　５　６　　　　　　　　
　　　　　　　　１　６　２

まず7224の内、72を28で割るのですが、
計算棒の各段には掛け算の例で示したように
28の倍数が９倍まで表示されていますので、
最も72に近くて、72を越えない
数56の指示数２を選びます、

　　　　　　　　　　　２　５　　　　　　　　　　　　　・
　　　２　８　) 　７　２　２　４　　　　　　　　　　　　
　　　　　　　　　５　６　　
　　　　　　　　　１　６　２
　　　　　　　　　１　４　０　　
　　　　　　　　　　　２　２　４

次に、162を28で割るのですが、
再び計算棒で28の倍数の内、162に近い数140の
指示数５を選びます、

　　　　　　　　　　　２　５　８　　
　　　２　８　) 　７　２　２　４
　　　　　　　　　５　６　　　　　　
　　　　　　　　　１　６　２
　　　　　　　　　１　４　０　　　
　　　　　　　　　　　２　２　４
　　　　　　　　　　　２　２　４
　　　　　　　　　　　　　　　０　　　　

この繰り返しで解を求めます。
　

平方根

平方根の計算には、平方根用の計算棒を併用します
開平計算は少し手数がかかりますが、筆算でも、
タイガー計算機でも、やはり、手間がかかるので
仕方ありません。

√126736=356　を計算してみます

まず開平計算なので２桁ごとに　くくります

最初１２なので暗算で３を立てます、

　　　　　　　　　３　　　　　　　　　　　　　　　　　　．
　　　　　　　１　２　６　７　３　６　　　
　　　　　　　　　９　　　　　　　　　　　　　　　　　　．
　　　　　　　　　３　６　７

ここからが計算棒の出番です
最初に立てた　３　の２倍、つまり６の計算棒と
平方根用の計算棒を用意します

今回　６の棒と、平方根棒の左の列を使います
適合するのは　５の段の３２５なので
５を立てます、

　　　　　　　　　　３　　　５　　　　　　　　　　　　　　．　　
　　　　　　　　１　２　６　７　３　６　　　　　　
　　　　　　　　　　９　　　　　　　　　　　　　　　　　　．
　　　　　　　　　　３　６　７　　　　　　　　　　　　　　　　
　　　　　　　　　　３　２　５　　　　　　　　　　　　　　．
　　　　　　　　　　　　４　２　３　６　　　　　　　　　　．

今度は、　３５と立てたので、この２倍　７０の
計算棒を用意します、
適合するのは　６の段の４２３６なので
６を立てます、

　　　　　　　　　　３　　　５　　　６　　　　　　　　　　．
　　　　　　　　１　２　６　７　３　６　　　　　
　　　　　　　　　　９　　　　　　　　　　　　　　　　　　．
　　　　　　　　　　３　６　７　　　　
　　　　　　　　　　３　２　５　　　　　　　　　　　　　　．
　　　　　　　　　　　　４　２　３　６　　　　　
　　　　　　　　　　　　４　２　３　６　　　　　　　　　　．
　　　　　　　　　　　　　　　　　　０

どうです、うまく計算できましたね。